Functions Describe the World: An Intro to Computer Science
The power of universal data encoding and computational universality
When I was learning to program I made flashcards from superficial things like syntax and memorised algorithms by heart. While this did help during the early stages of learning to code to help boost me past the chasm of incoherence, they became less and less useful over time as my knowledge about the practical details of programming languages was naturally reinforced through daily immersion in my code editor working on projects.

To my surprise, the flashcards I enjoy reviewing the most nowadays are the ones that don’t have obvious practical applications. These are flashcards like the ones I shared in my earlier article, which involve topics like the connections between logic and programming languages, Haskell, category theory, interactive theorem proving and so on. I see them as potential stepping stones towards new unexpected connections between ideas, with the power to transmute spontaneously from copper into gold.

As I wrote in my essay Spaced Repetition for Knowledge Creation:
Flashcards and the memories they encode are not isolated chunks but composable Lego bricks which can be glued together using rules of inference inside the universe's ultimate connection machine - the human brain… Each additional concept added to your memory creates another pathway for the brain's creative search algorithm to explore. As we grow our knowledge, we create a combinatorial explosion in the number of possible ways we can combine bits of what we already know to create new knowledge and solve problems.
So this article will be focused on abstract ideas and concepts. If you don’t enjoy it, try reading my practical guide to learning to program instead. I’m also busy working on a day-one programming tutorial to boost your knowledge to the point where you can start working on your own projects. If you are interested in reading the draft, please DM me on Twitter, I’d really appreciate your feedback.
Concepts
This guide prioritises fundamental, generally applicable concepts over practical details. There are so many good practical guides out there already, but the theoretical side of things is never explained well. The goal is to get you to understand the power of data and computation, and to inspire you to think of new ways to solve problems with computers.
Lots of different fields are becoming computational. For all fields X there’s a computational X… with the rise of AI, the question becomes - what do you learn? The under-the-hood mechanics of programming are becoming less important. What you need is a notion of what's computationally possible so you can guide AI to fill in the details. - paraphrased from Lex Fridman’s podcast with Stephen Wolfram
Instead of providing pre-made flashcards, I decided to record a video showing how I’d go about reading and turning what I wrote into flashcards. Check it out here:
Numbers and Data
You probably already know that computers use binary strings - long sequences of 0s and 1s - to store data. A computer’s memory is just like an extremely long column of cells in an Excel spreadsheet, each containing a sequence of 0s and 1s, where each 0 or 1 is called a bit (binary digit).
Why do computers use binary? Why not use a number system with a different base? One reason is that it’s simply convenient from a physical hardware perspective where these two states can easily be represented by two distinct and stable levels of voltage (eg. 5 volts for '1', 0 volts for '0'). This makes the computer more resistant to small fluctuations in power supply than if you had more states with smaller increments in voltage between them.
But leaving aside practical concerns, could you in theory create a computer using a different base, like base 10, the “normal” number system we use daily? How about the most minimal possible number system, unary? I want to show you that the exact “substrate” used doesn’t matter so long as it supports universal data encoding and computational universality.
Can we build a unary computer?
By unary, I’m referring to a tally-mark number system with just a single symbol. For example:
I = 1
II = 2
III = 3
…
Computers need to represent lots of different kinds of data - text, video, audio, genomic sequences, financial data and so on. Ideally, our system should be capable of representing any kind of data, a property that I will refer to as universal data encoding, the first of two kinds of universality that you will learn about in this guide. In modern computers, this is achieved by coming up with ways to associate strings of binary code with something we’d like to do computations over, like text and images. Can a tally-mark computer do this?
Let’s start with a very basic form of data - numbers.
We can easily create a one-to-one mapping between tally marks and integers greater than or equal to one by adopting the primary school interpretation of tally marks as above.
I = 1
II = 2
III = 3
…
But how can we represent any number (0, -24, 43.234, π…)? You might notice a couple of issues. To begin with, our current system doesn’t support the concept of the absence of a value. You are forced to start counting from one. How about this - let’s use a convention where we interpret the single tally mark as 0 instead of 1.
I = 0
II = 1
III = 2
…
That solves that. We’ve successfully created a one-to-one mapping from tally marks to the set of natural numbers. The invention of this new convention is more significant than it seems at first glance. We began by viewing sequences of “I”s as integers greater than or equal to one, then we discarded that view and adopted a new convention of treating the single tally mark “I” as zero. We now have two equally valid interpretations of tally marks depending on the lens we choose to look through. The point here is that the symbol “I” and sequences of “I“s are meaningless - it’s up to us to imbue them with meaning.
The mathematics that follows is not essential to understand so if it doesn’t seem interesting, skip to the conclusion, titled “Universal Data Encoding” where I have distilled out the main nuggets.
Can tally marks represent any number?
Negative Numbers
I = 0
II = 1
III = 2
…
How on earth will we represent negative numbers? If we were allowed to introduce a new symbol like + or - then it would be trivial, but let’s assume we aren’t. How could the positive side of the number line also fit the negative numbers into it? It’s as if we need to find a way to fold the full number line into itself with 0 as the crease.
Here’s a clever (and slightly mind-bending) idea. We know that there are infinitely many even numbers. Agree?
2, 4, 6, 8, 10…
We also know that there are infinitely many odd numbers.
1, 3, 5, 7, 9…
We can pair up even tally marks with negative numbers and odd tally marks with positive numbers.
I = 0
II = -1
III = 1
IIII = -2
…
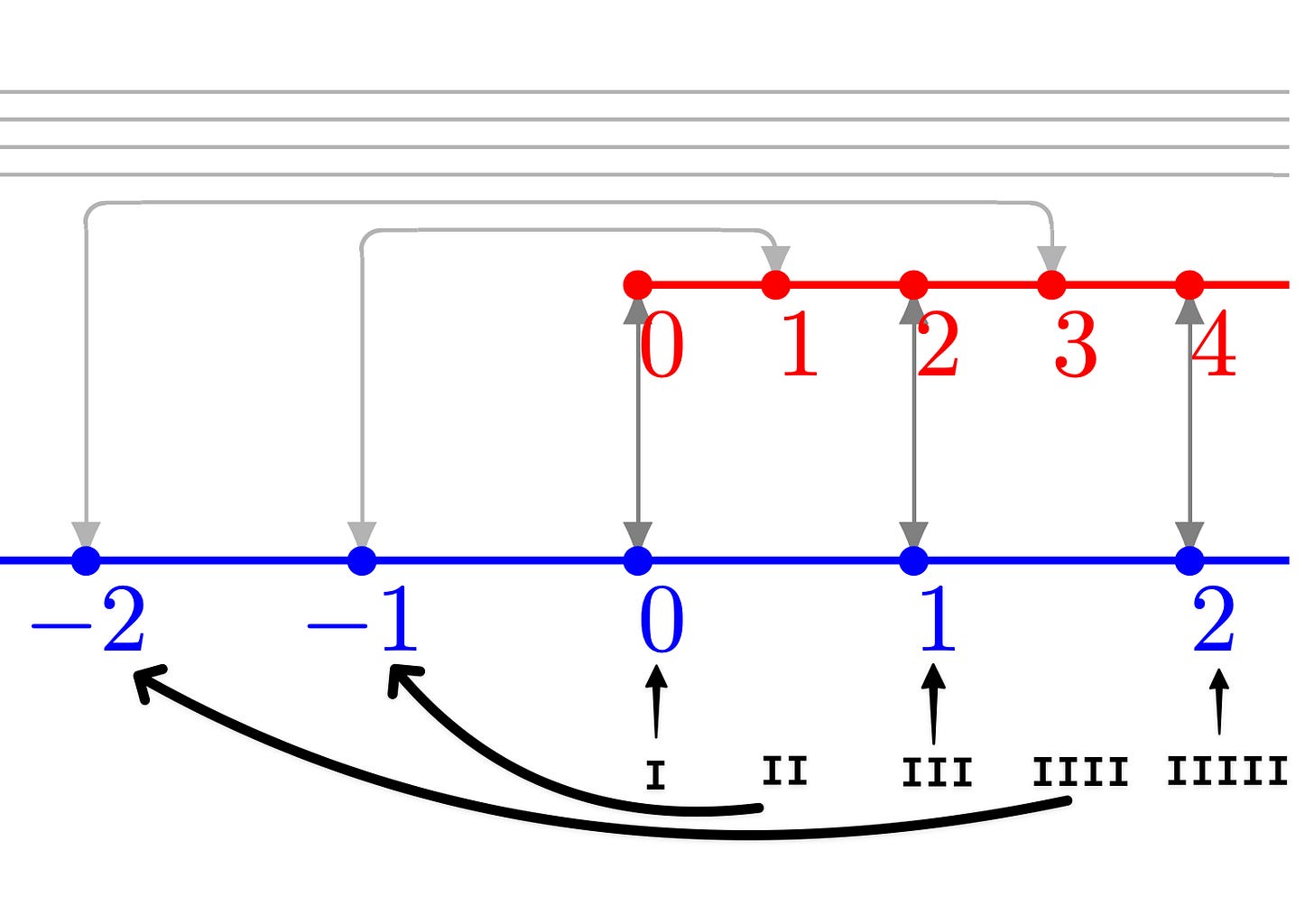
It doesn’t make sense at first that the counting numbers (0, 1, 2, 3…) or tally-marks could be put in one-to-one correspondence with a set of objects like the integers which seems much larger (…, -2, -1, 0, 1, 2, 3…) because it includes negative numbers. But these sets are actually the same size! Instead of thinking about these sets as sets of numbers, try thinking about them purely in terms of symbols - how many unique sequences can you create with tally marks (one symbol) vs integers (ten number symbols, plus a negative symbol)? You realise that you don’t gain any extra “power” from the different number symbols over just a single tally mark, because you can always create a unique sequence of tally marks to represent the number expressed using extra symbols. Therefore at their core, the power they wield to symbolically represent data is equally general.
Rational Numbers
What about rational numbers, like ½ and ⅔? Like the natural numbers, they also extend infinitely into the horizon along the number line, but they also have infinite depth, burrowing down into the number line, filling in the cracks between the natural numbers.
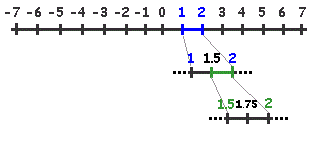
It seems even more implausible that we could create a mapping between tally marks and the rational numbers. But consider this: we know that rational numbers are always just pairs of integers written as fractions like x/y. We’ve already shown that we can map one-to-one between tally marks and integers, so surely it must be possible to map between tally marks and pairs of integers. Indeed we can use something called the Cantor pairing function to achieve this. It’s a function that takes two natural numbers as arguments and returns a unique natural number. See the following illustration.
Each point (x, y) represents the fraction x/y. The x is one natural number. The y is the second natural number. The arrows show a path that winds through every possible fraction x/y exactly once, showing a systematic way to list all fractions. In other words showing that the set of all fractions is countable. This demonstrates the counterintuitive fact that the set of rational numbers is not "larger" than the set of natural numbers. Since we’ve shown already that tally marks are sufficient to encode the natural numbers, they must also transitively be capable of representing rational numbers too!
Irrational Numbers
Finally let’s look at irrational numbers like π. Irrational numbers have decimals that can go on forever without repeating themselves. Here we hit a small roadblock which is that the set of irrational numbers has a strictly higher size (cardinality) than the natural numbers, famously shown by Georg Cantor using his Diagonal Argument. He showed that there are different sizes of infinity so we can’t put tally marks into one-to-one correspondence with the set of irrational numbers. In other words, they are uncountable.
But we can use rational numbers to approximate irrational numbers to arbitrarily fine detail. For example, the fraction 22⁄7 is a pretty good approximation to 𝝅. We can get closer and closer by using a continued fraction.
You can think of it like using polygons to approximate a circle, a technique invented by Archimedes back in ancient Greece. The more sides you add to the polygon, the better the approximation to the ideal circle. Visualise it here.
This is how computers approximate irrational numbers. It’s not possible to perfectly encode them, but just as we can get close enough approximations to circles by adding more and more sides to polygons, we can get as close as we like to irrational numbers by adding more and more computer memory.
Universal Data Encoding
Above we used all kinds of mathematical tricks and creative interpretations of tally marks to represent different kinds of numbers. We showed that just a single symbol is sufficient to encode any sequence created from a finite alphabet of symbols. While we started with the “common sense” primary school interpretation of tally marks representing integers greater than or equal to one, by the end of the section, the tally marks were mere symbols to which we ascribed new interpretations to get them to represent (or at least approximate) any number we wanted. This shows us that data is in the eye of the beholder: it's the role of programs to interpret otherwise meaningless symbols into something useful.
Some of the most important inventions are those that figure out how to create clever mappings between symbols and meaningful structures. Of course, there are the obvious examples like text, images and video. But we can also view things like the genetic sequence through this lens.
Mother nature came upon universality long before we re-discovered it. Using the four base pairs A C G and T, DNA can encode the instructions to make a T-Rex or a chicken. It can even contain the source code for the most complex creation in the known universe: the human brain. - Universality and APIs
Consider also the recent advances in large language models. Researchers figured out how to map semantic meaning from text into vectors of numbers called text embeddings.
But we haven’t created mappings for all of the things we’d like to do computations over. Take the human brain for instance - there are so many cognitive phenomena that remain inaccessible to modern-day computers. We can’t create, read and update human memories. Nor can we compute over subjective states like feelings and emotions. Once science advances to the point where we understand the brain better, we will create these new mappings. A whole new class of computations will become accessible, and many problems will be solved as a result.
We showed above that just a single symbol - a tally mark - is sufficient to represent any data. So what do we need binary for? Why use two symbols (0 and 1) if one symbol suffices? Well, there’s another kind of universality we care about, namely computational universality: the ability to simulate any other computational system or algorithm, given enough time and resources.
Computational Universality
The beauty of binary numbers is that just like tally marks, binary strings like “01001000 01000101 01001100 01001100 01001111“ don’t have any pre-determined meaning and can be used to encode any data. But beyond that, the big advantage of binary is that it supports enough distinguishable states (two) to achieve a second jump to universality allowing a computer to perform any computable algorithm. By computable algorithm, what we mean is a sequence of instructions of finite length that a rule-following entity (human, computer or otherwise) can perform. For example, a cooking recipe fits this description.
To understand why binary can do this and our tally mark computer can’t, let’s examine the classic model of computation called the Turing machine.
Turing’s Machine
…the model of computation that [Alan Turing] used was physical strips of paper divided into squares with symbols and a finite set of discrete operations on them - The Universal Turing Machine…
The classic abstract model of computation is the Turing machine, conceptualised by British mathematician Alan Turing in the 1930s. In his paper, Turing imagined a machine with a scanner head which could read and write symbols to and from a tape of infinite length.
At each step, the machine takes the following actions:
1) Read the symbol on the tape in the current cell.
2) Follow instructions based on its current state:
Write a new symbol to the tape to the current cell (which can be the same as the current symbol).
Transition to a new state (which can be the same as the last state).
Move its head left or right.
At any point in time, the machine is in one of a finite number of states which determines how the machine behaves. The current state provides instructions for what to do next upon reading a particular symbol. Reading a symbol in one state could result in a completely different action in another. In other words, the machine’s set of internal states defines a mapping between data and behaviour.
The Turing machine’s states are analogous to the different lenses we swapped between above when discussing tally marks. Swapping between the primary school view of tally marks as counting numbers and a new interpretation is akin to a state transition in the Turing machine. States are lenses through which to interpret otherwise meaningless strings of symbols into something meaningful.
Turing himself did not use binary for his machine, he allowed for a variety of symbols, but as we showed above, one symbol is enough to encode any data, so why didn’t he just use a single tally mark instead?
The reason is quite simple: say you have a tally mark computer and you want to increment a natural number encoded as a tally mark sequence on the tape. Incrementing a tally mark number is a simple operation, all you need to do is find the end of the sequence and add an additional mark.
But you immediately realise that there's no way to find the end of the tally mark number because all cells in the infinitely long tape contain tally marks! Suppose we added a blank symbol to represent the ends of numbers, but then we are effectively using two symbols instead of one and we are no longer operating with a tally mark computer.
In theory, we could hardcode the states of the machine such that it could perform the increment operation perfectly for one particular number. But it would not generalise to any number. You would need an infinite number of sets of states to encode the increment operation for every possible length of tally mark sequences.
I + I
II + I
III + I
…
And of course it would not be easy to distinguish the output of the increment operation from the rest of the tape, since every cell already contains a mark!
Adding an extra symbol allows the machine to make the leap to universality.
IIIIIIII000000
Assume the machine starts on the first I.
if (cell == I) {
moveRight()
}
else {
eraseCell()
writeCell(I)
}Clearly this algorithm (which can easily be implemented using states and state transitions in a Turing machine) works for any tally mark input. This is a small micro instance of the jump to universality afforded by the additional symbol. Suddenly we can use if-else statements and loops massively widening the set of programs we can express. This simple example undersells the true power of computational universality.
In Claude Shannon’s paper, "A Universal Turing Machine with Two States", he showed that a machine with two symbols can perform the exact same computations as a machine with more symbols. In other words, both machines are universal, and while certain computations may be more convenient to express using more symbols, there’s no fundamental difference in power or generality between the two. Shannon hinted that there is a correspondence of motion of the machine head in machine A and the machine head in machine B - one machine simulates another by mapping its head movements to that of the other machine. This correspondence between physical movement turned out to be a deep and fundamental connection between computer science and physics, grounding Turing’s abstract mathematical model of computation in reality.
Functions Describe the World
FUNCTIONS DESCRIBE THE WOOOORLD
An important detail to notice about Turing’s model of computation is that it’s a physical process. This is obvious in hindsight from his description of the Turing machine but was not fully appreciated until 1985 when physicist David Deutsch published a paper making the connection explicit.
It is argued that underlying the Church-Turing hypothesis there is an implicit physical assertion… - Quantum theory, the Church-Turing principle and the universal quantum computer
the phrase [Turing] used was that [the Turing machine] could compute anything which would naturally be regarded as computable… he meant computable in nature by physical objects. - David Deutsch Dirac medal speech
The significance of computation being a physical process is that it must obey the laws of physics. Therefore what we can achieve through computation is only bounded by what is physically possible in our universe.
It also happens that the laws of physics (at least as we currently understand them) are themselves computable because they only refer to computable functions. This is interesting because you can define plenty of non-computable functions in abstract mathematics. But none of our best theories of physics seem to depend on them.
If instead [the laws of physics] were based on, say, Turing machines as elementary objects instead of points and so on, and if the laws of motion depended on functions like “does this halt?” instead of on differential equations then one could compute using operations which with our physics we call non-computable. - What is Computation? (How) Does Nature Compute?
If the laws of physics are computable and we can create universal computers capable of performing any computable function, then we must be in principle capable of simulating any physical object or process. The closer our theories of physics get to the true laws governing our universe, and the closer our computers get to the ideal universal computer, the better the approximation.
This property of computation applies to many areas of science like climate science and drug discovery which depend on creating better and better simulations of weather systems and molecular interactions. But there’s one object we might like to simulate more than any other - the human brain. While the brain is a very complex physical system, as long as you don’t believe that the brain has supernatural properties or is powered by magic, then you must recognise that all cognitive processes, like thinking, consciousness, proving mathematical theorems, creativity, art, music and so on depend on physical processes which a universal computer is in principle capable of simulating to arbitrarily fine detail. In other words, there’s nothing in the laws of physics preventing us from writing computer programs that can match the intelligence of humans.
Next Steps
I hope you enjoyed my introduction to computer science. If you have any feedback, please comment or send me a direct message on Twitter.